The Physics of Harpsichord Sound
In 1977, Fletcher judged that the sound of harpsichords seemed well within the purview of known physics and that "a relatively complete first-order study should be feasible." The study was begun by Savage et.al. This page, and related ones, are to continue their work a bit.
Unlike Fletcher and Savage, however, I no longer have access to a fully equipped laboratory as I used to. And, I don't have a harpsichord that I will treat the way Savage did his! My instrument is my life. So, I have chosen methods that any harpsichord builder or owner can replicate, and hope to describe them sufficiently clearly that they can. A true understanding of harpsichord sound and construction requires the expertise of builder, player and physicist together. I welcome collaborators.
Where does the energy of a harpsichord string go?
The relevant properties of the c' string of my harpsichord are shown at right - all but the density of the wire are direct measurements.
I measured the compliance of the soundboard by placing a reference beam across the sides, adding a 1 kg weight to the bridge next to the c' string (carefully!), and measuring the deflection of the bridge pin compared to the beam with a dial caliper: 0.0126 cm, k = 7.8x107 dynes/cm.
Tap tones of the bridge were recorded digitally with a SoundBlaster 32 soundcard - a typical Fourier transform is shown at right. To first order, the resonant frequency can be taken as 110 Hz.
Assuming the thickness of the soundboard (which I can't measure non-destructively) to be the usual 0.3 cm density 0.45, and calculating the mass of the bridge from its measurements and the density of beech 0.64, the mass of the soundboard is about 0.21 g/cm2. (60% of this is soundboard, 34% bridge, 6% strings).
The decay rate of the c' sound was measured by recording the sound with the soundcard and fitting the waveform envelope graphically with an exponential: 2.6/s.
Theory
From (1), the acoustic mass of the soundboard at c' is 7.8x107/(6.28x110)2 = 163 g.
The wave equations for a string (equation 11 on the bridge pin page) say that the effective length of a string terminated by this mass and the measured compliance is 1.33x10-2 cm shorter than that of a perfectly terminated string at 260 Hz, which implies a soundboard/string amplitude ratio of pi/L times this, r = 6.3x10-4.
One energy loss of harpsichord strings is due to the viscosity (stickiness) of air, which is approximately given by (2). A graph of this equation is shown at right - it's a strong function of wire diameter. For my c' string, the loss rate works out to 0.86/s at 260 Hz. The observed sound loss rate being 2.6/s, that means that 33% of the 1st partial string energy is turned into heat in the air surrounding the wire, leaving 1.7/s for the soundboard. The loss rate increases for higher partials, so the sound of higher partials will die away faster than lower ones.
Given the estimated soundboard mass of 0.21 g/cm2, the effective radiating area (of a rigid piston perturbing a sphere) should be roughly 163/.21 = 776 cm2, about 10% of the total soundboard area.
The amplitudes of the partials of the vibrating string are given by (5). The 1st partial amplitude is 0.13 cm, so the corresponding string energy at pluck from (3) is 5.9x103 erg, of which 3.9x103 erg can reach the soundboard.
The acoustic power radiated from a spherical source (harpsichords have closed bottoms) is given by (4), where V is the volume amplitude 776x0.13 r : 40 erg/s for the 1st partial, 94 erg/s summed over all partials. The minimum audible sound is usually taken as 10-5 erg/s (1 pW) at 1 m, so this works out to 70 dBa (the volume of an average human speaking voice - maybe low.) The total 1st partial energy radiated as sound by the soundboard should be 40/2.6 =15 erg. Summing over all partials (allowing for the increase in viscous loss with frequency, but assuming the soundboard has constant properties) gives 34 erg total. The energy input to the string by the pluck being 9000 erg, the overall acoustic efficiency of the instrument should be 0.4%. The rest of the energy not absorbed by air viscosity (66%) must just warm up the soundboard.
The acoustic power radiated directly by the string (as a dipole) is approximately (6) for the 1st partial, lower for higher partials since the dipoles themselves form dipoles. It is very small.
A calibrated sound level meter would be needed to check this in the traditional way. But, I can check relative overall partial strengths with the sound card.
Spectral Power Measurements
The instrument was set up so that strings other than the single string being recorded were damped (including the 8' bridge-hitch ends). A complete c' sound from pluck to inaudibility was recorded (44k samples/s 8 bit) with a microphone 1 m from the bridge pin. (As you can see, computer sound cards have a lot of hum and noise - Fourier transforms are essential to working with them. I have to assume that the response of the condenser microphone plus card is flat, as I've no way of checking it now.) Partials can easily be distinguished up to 10 kHz.
Fourier transforms were then done in successive 0.1 s chunks for each partial. For each chunk, the volume was levelled by the inverse of the overall decay function (2.6/s) so each value is an average over the 0.1 period. A typical chunk transform is shown - the signal/noise ratio is adequate even for a 0.1 s sample at 3 s after the pluck. From these chunk transforms, the relative radiated power of each partial was calculated, and is shown compared with the theory for a non-resonant 'piston' soundboard. ((4),(5), equation (11) on the bridge pin page). The soundboard seems to be acting primarily as a non-resonant element. And, it seems close to being a rigid piston, thus far more effective at radiating high partials than low.
As you can see, partials 1 and 3 are lower in power, and the high partials a bit higher in power than expected. That should be due to the deviations of the soundboard from those of a piston, i.e its resonances.
There are two ways of determining the frequency response of a soundboard. One is by applying a force at a series of frequencies over the range of interest and measuring the sound radiated for each. The other involves applying an impulse - a force short in period compared to the maximum frequency of interest - and taking the Fourier transform of the resulting sound. With expensive lab equipment, the first method gives more reliable results, but the second can be done with just a finger and ear, as instrument makers have traditionally done.
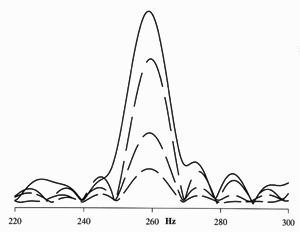
The soundboard acoustic mass being 163 g, its lowest resonant frequency 110 Hz, and the highest frequency of interest here being the 24th partial of c', 5240 Hz, the mass of the object applying the impulse should be about 163*110/5240 = 3 g. The lighter the striking object, the harder it is to get enough energy into the soundboard to record. I stuck a tiny beech anvil to the bridge with fish glue (removable), and, after a few experiments, tapped it with the back edge of a steak knife blade, near the end where the effective weight is roughly 3 g (calculated from the density of steel 7.8 g/cm²). With a bit of practise, I was able to hit so that the elastic rebound of the anvil threw the blade clear of the soundboard, that is with no double-hit. A typical spectrum is shown at right. As a check, I took one with a 25 g jeweller's hammer as well - in theory it should excite to a maximum of 110*163/25 = 700 Hz; as you can see that's about what it does. The same spectrum for a traditional finger tap shows why instrument makers use it - it is the best way to identify the pitch of the lowest resonances.
Even with the knife blade, I found the spectra beyond partial 16 very dependent upon the exact strike dynamic - the dip at partial 21 appears other places in other trials. Still, the result is good enough to show why the 1st partial of c' is lower than theory based on a non-resonant soundboard, and why partials 8-16 are higher. So, I'm satisfied that the theory above describes to first order where the energy of a harpsichord string goes.
John Sankey 1999
other notes on physics
P.M.Morse, Vibration and Sound. 1936.
N.H.Fletcher, Analysis of the Design and Performance of Harpsichords. Acustica 37,139 1977.
M.Goodway & J.S.Odell, The Metallurgy of 17- and 18th-century music wire. 1987.
W.R.Savage et.al, Air and structural modes of a harpsichord. JASA 91(4):2180-9 1992.
N.H.Fletcher & T.D.Rossing, The Physics of Musical Instruments. 1998. There is an error in the viscosity damping equation in both their 1st and 2nd edition (a different error in each).


tap tone spectrum
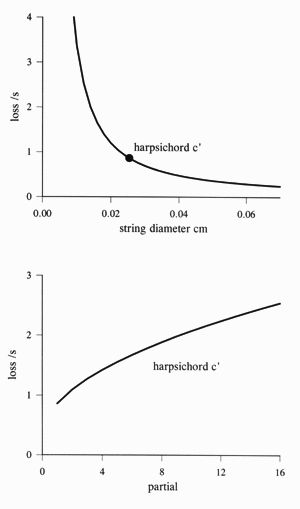
air viscosity loss (energy)
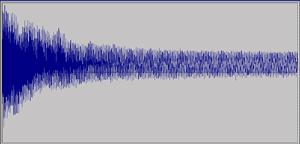
the recorded waveform (3 s, amplitude)
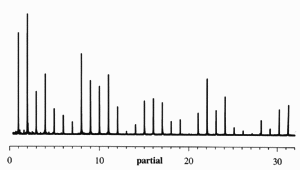
the frequency spectrum (amplitude)
partial 1 transforms at 0,1,2,3 s
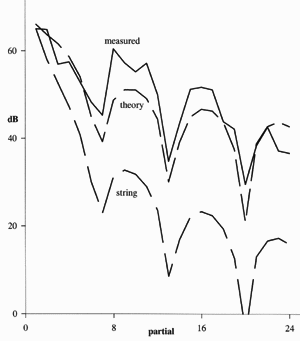
relative partial powers

impulse spectra