Most stringed instruments terminate the string at one point at each end, in a small notch in a bridge. In particular, the ancestor of the harpsichord, the medieval (pre-1400) psaltery did - its strings are always shown crossing a bridge in a straight line. But, the first detailed representation of a keyboard plucked instrument, that of Henri Arnault of Zwolle in 1440, shows the strings angling sharply at the bridge line, so sharply that a pin must have been used at this point rather than a notch, although Arnault does not show one. In surviving old northern harpsichords, this pin was placed a significant distance inside the bridge or nut; in Italian instruments it remained in the position apparently shown by Arnault, tight against the bridge peak.
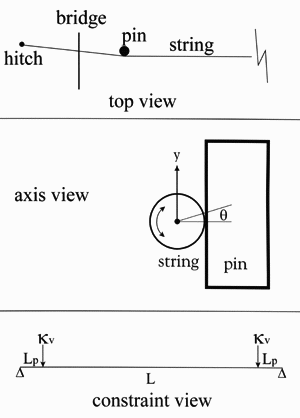
Viewing the system from the top, the string was held against the pin by the position of the hitch pin, which forced the string to change angle at the pin by about 0.1 radian. The horizontal force of string on pin was enough (typically 400 g) to prevent any sliding, rubbing or buzzing. The string made a similar angle in the vertical plane, which held the string equally firmly down against the bridge.
Viewing the pin-string contact along the axis of the string, the string was free to roll (not rub) up and down the pin as the string vibrated. The angle of the pin, whether or not it 'traps' the string, does not affect this (superposition theorem) as long as the metal is not stressed beyond its elastic (linear) limit. (If it were stressed that much, the string would break due to kinking or the pin would have notches in it, and old instruments don't have pin notches. Also, the wire bend at the pin applies a sideways twist to the bridge, which must be small to avoid warping the soundboard.) The vibration-related rolling was resisted by a spring force due to the torsional stiffness of the portion of the string between the pin and the bridge. The string was probably prevented from rolling along the bridge by the depression crushed in the wood by the string pressure, but I have to verify this.
What effect could such a structure have on the sound? It is far too consistently done in early instruments to be an accident. Harpsichord makers of today know well enough that pinning has a significant effect on the brightness or dullness of the tone. But, it seems that no one knows why. So, I decided to try to understand it.
To analyse such things, it helps to review the basic physics of stretched strings.
The motion of an ideal stretched string is obtained by solving the partial differential equation (1), where y is the displacement of the string, x the position along it, t time, and c the phase velocity of waves on the string. The phase velocity of an ideal string is given by (2), where m is the mass per unit length and T the tension. (1) has to be solved for the constraints (3), where L is the length of the string.
(1)+(3) has solutions only for discrete frequencies (4), where n is any integer. The values below (4) are typical of a c' string of a northern harpsichord strung in iron of the period.
For a well-played harpsichord, the velocity of the plectrum at the point of string release is small compared to the phase velocity on the string, so the amplitudes of the partials n may be obtained from (5), where y0(x) is the displacement of the string at the moment of release by the plectrum. Typical values for a c' string are given in the table (plucking point 1/7).
For a slightly stiff string, a perturbation solution of (1) may be obtained of form (6), showing that the frequency series n is no longer harmonic. The effect of stiffness may be most easily seen by putting the first inharmonicity term (the one in n²) in dimensionless form as in (7), where E is Young's modulus, S the stress (8), d the diameter of the string. For a harpsichord c' string, this term is sufficiently small that the string may be treated as being perfectly flexible.
So far, the string has been assumed to be perfectly terminated at two points and free otherwise. The pin is not a perfect termination, it's elastic in the vertical plane, which is the plane most tightly coupled to the soundboard.
The force the pin must apply to the string to twist it is given by (9), where J is the polar moment of inertia of a string (10), G is the shear modulus of the material, and Lp<<L the distance between pin and bridge. Typical values of Lp for a northern harpsichord c' string are 0.2 cm at the nut, 0.6 cm at the bridge. The depression in pin and wire due to the bearing force 0.1T is small, of the order of 0.1T/E, 3x10-7 cm, and the velocity of movement of the string on the pin is tiny compared to the speed of sound in metal. The rolling pressure of wire on pin should thus be lossless and not impede movement.
Solutions of (1) for symmetric elastic terminations are obtained from (11). As can be seen, the length of purely elastically terminated strings is independent of partial and the elastic forces at the termination add to give the effective length. (9-11) yield an elastic length increase of 0.32 cm at the nut, 0.99 cm at the bridge. Since length change is reciprocal to elasticity, the vertical sounding length of the string is 1/(1/.2+1/.32)+1/(1/.6+1/.99)=0.50 cm longer than the pin-pin length. The soundboard has a small effect compared to this - at c' my Ross has a vertical compliance of 7.8x107 dynes/cm and a resonant frequency about 110 Hz. The acoustic mass is thus 163 g and the effective length change due to the soundboard is only -.013 cm.
In the horizontal plane, the string support is different. A typical pin is of yellow brass, about 0.1 cm in diameter and 1 cm long. In good instruments, the string contact point is close to the bridge wood, usually about 0.1 cm above it. The horizontal elasticity due to the pin is approximately (12), where dp is the diameter of the pin, ev the height of the string above the bridge, dv the depth to which the pin is embedded in the bridge, Ew the elastic modulus of the bridge wood, and Eb that of brass. (The elastic modulus of beech is about a tenth that of yellow brass.) A finite-element integration of the stress in the wood about the pin shows that the correction to (12) due to stress concentration in the wood is small. The pin support is rigid in the horizontal plane compared to the vertical.
So, the natural (unforced) vertical frequency of the string is 0.8% lower than the natural horizontal frequency. (All this assumes, of course, that the string does not buzz on the portion of the bridge that holds the pin, that the pin is not so heavy that it mutes the sound, nor so flexible or so loosely seated in the bridge that it fails to hold the string firmly. Repair shops regularly see all of these in instruments built from kits.)
Such a situation has been dealt with by Weinreich (JASA 62(6):1474 1977) in connection with the unison tuning of pianos. His theory predicts that two strings can sustain longer than one string, if they are tuned to different natural frequencies but are constrained by their coupling to the soundboard to move at a common frequency.
Are the vertical and horizontal vibrations of a harpsichord string sufficiently tightly coupled for the Weinreich effect to occur? I don't know how to calculate that. However, my son Michael had a school assignment for which this investigation qualified. (It was an archaeology course - he proposed to 'dig up the sound of old harpsichords' and got an A+ and a class prize :-) So, he built a monochord to see if experimental evidence could be obtained that the Weinreich effect applies to a single harpsichord string. The soundboard thickness and width, bridge dimensions, and string diameter were typical of a northern c' string, although the total soundboard area is less. The bridge was designed to permit varying the bridge-pin distance while keeping all other pin and string properties constant. The sounds were recorded digitally with a PC sound card for analysis.
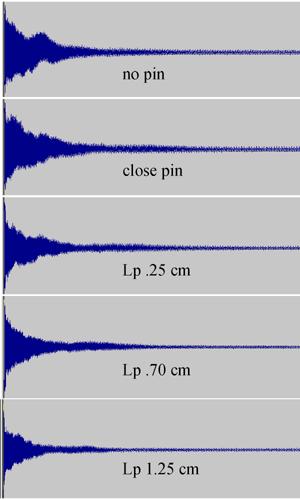
A 4 s sample of 5 pin-bridge geometries is shown at right. The amplitude envelopes show clearly that there are indeed two coupled vibrating entities, very close in frequency with no pin, a bit faster beats with a close (Italian) pin, and much faster for pin-bridge distances 0.7 cm or greater. With only one string on the instrument, they can only be horizontal and vertical planes of vibration. The effect was the same with small and moderate plucking, so it is not the tension-coupled precession of polarization, which increases as the square of amplitude. And, using a stereo microphone hookup, the phase relationships of the two channels show that the two planes radiate from different areas of the monocord, just as Weinreich found for a piano. So, Weinreich's effect does apply to harpsichords.
Also, the envelopes show that the sound volume after the string vibration settles down from the pluck is less the greater the pin-bridge spacing, particularly for pin-bridge distances 0.7 cm or greater. An aural comparison of the sounds of the various geometries indicates that it is the fundamental that suffers most in power with large pin-bridge spacing.
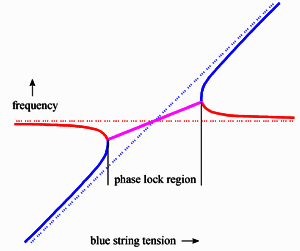
An illustration of what happens is shown at right (adapted from Weinreich). When the blue string of a unison pair is tuned close to the red string in frequency, the dotted lines show the string frequencies if the strings are independent. When they are coupled together and tuned close in frequency, they will follow the solid curves, and over a central region join together to generate a single frequency (magenta). As Weinreich showed, when the strings are tuned as at either end of the magenta line, they sustain longer than if they are tuned as at the center of the magenta. When the red and blue are the horizontal and vertical planes of a single string, moving the bridge pin changes the coupling between the two planes as well as the frequency difference - the picture is not as clear as with two separate strings of constant coupling, but it's the same effect.
Of course, early makers used their ears, not the math and technology available to us today. The monocord sound with no pin and the close pin are almost indistinguishable, both being full with a distinct pop at the beginning. The pin-bridge separation of 0.25 cm still sounds full, but has a more even decay of sound than the first two. At 0.70 cm separation, the sound is very close to that at 0.25 cm but slightly more nasal, and no pop is left; at 1.25 cm, it is thin to the point of sounding false.
So, the sound variation resulting from variation of pin-bridge length is clearly audible. But, because it results from a coupling between two planes of vibration of a string, the 'best' position will depend partly on a very elusive parameter, the acoustic coupling between those two planes provided by a soundboard-bridge system. (Most of the coupling will be via the Poisson effect and the rotation caused by the rolling, in the region of 20%. The coupling between two adjacent strings on a soundboard, the situation Weinrich dealt with, is less than 1%; that's why the frequency difference between the two directions of a string can be so much greater than that between two piano strings.) A maker who wishes the characteristic northern harpsichord sound should expect to experiment with any new model, increasing the pin-bridge distance until the sound just starts to go thin, then backing up one step. The best distance may be expected to be roughly 1/100th of the string length over the upper portion of the range where scale is constant. But, keep it small rather than large.
Part of the typical Italian sound results from the closeness of pin to bridge. The pin-bridge system, as opposed to a notched bridge, is an important part of northern tone, but seems to play little to no part in Italian tone. It is possible, therefore, that it is an element that was maintained by tradition in Italian instruments, rather than one organic to them, corroborating the evidence from literature that harpsichords originated in the north, then moved south to Italy.
Anyway, when you set pins in a northern harpsichord bridge, you now know one thing to listen for, and why.
geometry

equations
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| A | .718 | .323 | .179 | .101 | .052 | .020 | .000 |
| n | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| A | .011 | .016 | .016 | .013 | .009 | .004 | .000 |
partial strengths at pluck

the monocord bridge with varying pin-bridge distances

the monocord, recording
sound amplitude envelopes
phase-locking of two strings on a soundboard