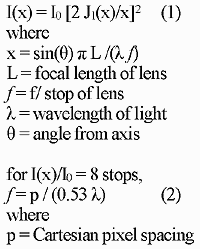The f/# above which diffraction begins to cause visible softening of digital camera images equals the pixel spacing in micrometers times 1.4
Details
Diffraction occurs when light encounters any change in optical properties. This note considers it in photography, specifically what occurs when light passes through a circular aperture, the iris that determines the lens f/#.
The effect on light of such an aperture is given by equation (1) at right. A plot of this equation is shown below it.
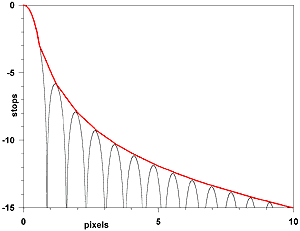
Astronomers, who deal with perfect point objects, are concerned with the detailed black curve and define resolution by the first minimum in that curve at x=3.83.
Photographers looking at normal scenes with extended objects are concerned only with the red envelope curve. Our most useful definition of diffraction-limited resolution is the point at which contrast in an image is greater than 8 stops, the maximum handled by most photographic media. That occurs at x=8.8; values greater than that will not affect the bite of our images. Note that bite as defined here is different from resolution, which simply determines whether or not a detail is visible. Resolution loss can be replaced by post-processing sharpening; bite isn't.
Resolution of a digital camera is limited by the spacing of its sensor pixels, 8.45 µm for the Nikon D700. And here a complication arises: sensors can only output one intensity value. So, they have to have filters on them to resolve differing colours. Most colour cameras today use the Bayer layout shown at right. The effective pixel spacing of the green sensors is 1.4 times the Cartesian pixel spacing, of the red and blue sensors, twice the Cartesian spacing. The effective D700 pixel spacing is thus at best 12 µm. In practise, interpolation algorithms fall a bit short of this, as will be shown below.
Defining the angle from the axis in (1) as one pixel results in an important result shown in equation (2): diffraction at the image does not depend on the focal length of the lens, it depends solely on the f/#, effective pixel spacing and the wavelength of light. That may seem counter-intuitive except to another physicist, so here are four images of a sharp white edge, each at f/22, taken with four lenses ranging from 14 mm focal length to 180 mm:

At a light wavelength of 550 nm (the middle wavelength of green light), equation (2) shows that diffraction is one pixel, with an ideal lens and Bayer interpolator, when the f/# equals the Cartesian pixel spacing in micrometers, - f/8 for the D700. The softness will be proportional to f/#, that is f/16 will give 2 pixels softness, f/32, 4 pixels. It also means that a DX (23.7x15.7 mm) camera such as the D300 has 1.6 times the diffraction of an FX (36x23.9 mm) camera when it takes the same picture at the same f/# and resolution, because the pixels have to be 1.6x smaller to fit in the smaller DX frame.
Real lenses have resolution limits in addition to diffraction, and irises that are not perfect edges or circles. And, it's necessary to find out how effective the Nikon interpolation algorithm is. So, I ran tests on one of my sharpest lenses, a Nikon 70-180 mm macro, at 180 mm focal length and an object distance of 2 m. A target was prepared with a clean white edge, mounted on a doorway and lit so that the contrast between white and background at the edge was about 15 stops. Focussing was by magnified liveview, TIFF and NEF photos taken at ISO 400 with no noise reduction, then enlarged so individual camera pixels are visible.
The results are at right. As you can see, the 8 stop resolution with the lens wide open is about 3 pixels. This is not due to lens imperfections, its source is the Bayer interpolation in the camera. Here is an unprocessed raw sensor image at f/5.6 with the pixel colours marked. It shows that the lens itself is as sharp as the pixel array can record. It also puts to rest concerns that the anti-aliasing filter of the D700 impairs camera resolution, it obviously doesn't.

The image at right for f/32, processed the way the camera processes our images, shows about 5 pixels width at 8 stops. 3 pixels (the Bayer softness) convolved with 4 pixels (expected diffraction softness) is 5 pixels, exactly what is observed. So, the theory above is well matched by experiment.
So, based on these experiments, my guideline for the f/# above which diffraction begins to cause visible softening of Nikon digital camera images is:
f/# equals the pixel spacing in µm times 1.4
That is, above f/11 for the D3/700, above f/8 for the D3x/300/800.
Of course, this doesn't mean that this is the only aperture to use! Close macro work may require increasing it to increase depth of field, subject isolation, portraits in particular, often benefit from decreasing it. But, for maximum bite, set your camera there and change it only when there's a photographic reason.
Depth of field is the same for identical images taken from the same location no matter what the image size is. The diffraction and depth of field of an FX camera at 50 mm f/11 are the same as the diffraction and depth of field of the equivalent image taken with a DX camera at 35 mm f/8. Further, since the FX pixels are twice the area of DX pixels, the photons/pixel (noise) will be the same as well.
If you reduce the pixel size of your photo by 2x, commonly done when posting on the web, the effective pixel size is doubled, so diffraction won't be visible until above f/22 for a D700.
Effective f/# in Macro Photography
A good approximation to the actual f# in macrophotography is the indicated f# multiplied by (1+M/p) where M is the magnification and p is the pupil magnification. p=1 for prime lenses in the 50-150 mm range, but must be measured for others. For retrofocus wide-angle lenses, p>1; for true telephoto lenses, p<1. The pupil magnification can be estimated by looking into the front and rear of the lens and measuring the diameters of the apparent apertures: p equals the entrance pupil diameter divided by the exit pupil diameter. When a lens is reversed, so are the pupils, p=0.45 for my 20 mm lens when reversed. If you use two afocally coupled lenses, the rear long focal length lens should be wide open to avoid vignetting and the aperture controlled with the front short one; the formula given applies to the front lens f#.